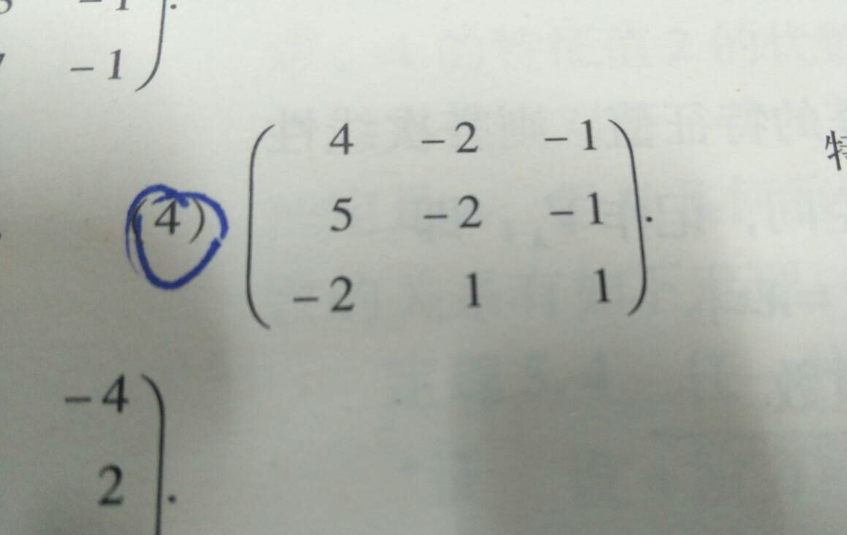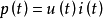ijk向量叉乘计算公式怎么记

ijk向量叉乘计算公式怎么记

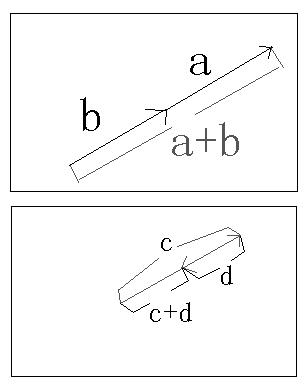
将向量用坐标表示（三维向量），若向量a=(a1，b1，c1)，向量b=(a2，b2，c2)，则向量a×向量b=|ijk||a1b1c1||a2b2 c2|=(b1c2-b2c1，c1a2-a1c2，a1b2-a2b1)（i、j、k分别为空间中相互垂直的三条坐标轴的单位向量）。叉乘，也叫向量的外积、向量积。顾名思让芦义，求下来的结果是一个向量，记这个向量为c。向量c的方向与a，b所在的平面垂直，且方向要用“右手法则”判断（用右手的四指先表示向量a的方向，然后手指朝着手心的方向摆动到向量b的方向，大拇指所指的方向就是向量c的方向）。因此向量的外积不遵守乘法交换率，因为向量a×向量b=-向量b×向量a在物理学中，已知力与力臂求力矩，就是向量的外积，即叉乘。一般我们在解决立体几何题目时会选择建立坐标系，因为这样做比较保险也有固定套路。很多时候这些题目要求你计算某一个面的法向量(normal vector)，这在高中阶段也是有固定方法的，我们这里想要介绍的是一种更高级也更迅速的方法，也就是引入向量叉乘(cross product，“向量”同物理中的“矢量”概念，一直想不通为啥数学和物理用不一样的名字，英文都是vector)这一概念。我们都学过向量的标量积，也就是坦销带所谓的点乘(dot product)，两个向量做标量积后得到的是一个标量。我们这里定义一种新的向量运算，也就是向量积或者叫叉乘:其运算结果仍是一个向量，我们记之为向量c，它的模定义为：其中θ为向量a和向量b的夹角，如下图所斗祥示，c的模即以a和b为两条边的平行四边形的面积。