双曲线渐近线公式是什么？

双曲线渐近线公式是什么？

y=±(b/a)x（当焦点在x轴上），y=±(a/b)x (焦点在y轴上）（a：双曲线的实半轴，b是虚半轴。长）

几何性质：

(1)范围：|x|≥a,y∈R。

(2)对称性：双曲线的对称性与椭圆完全相同，关于x轴、y轴及原点中心对称。

(3)顶点：两个顶点A1(-a,0),A2(a,0)，两顶点间的线段为实轴，长为2a，虚轴长为2b，且c2=a2+b2。与椭圆不同。

(4)渐近线：双曲线特有的性质，方程y=±(b/a)x（当焦点在x轴上态纳），y=±(a/b)x (焦点在y轴上）或令双曲线。

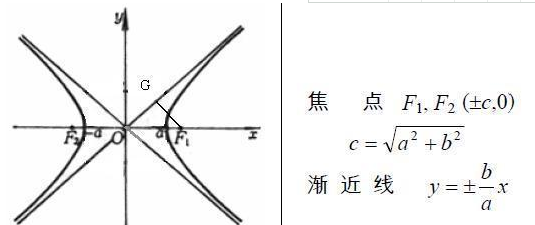
渐近线特点：

无限接近，但不可以相交。分为垂直渐近线、水平渐槐码近线和斜渐近线。

当曲线上一点M沿曲线无限远离原点时，如果M到一条直线的距离无限趋近于零，那么这条直线称为这条曲线的渐近线。

需要注意的是：并不是所有的曲线都有渐近线，渐近线反映了某些曲线在无限延伸时的变化情况。

根据渐近线的位置，可将渐近线分为三类：水平渐近线、垂直渐近线、斜渐铅闭哪近线。

y=k/x(k≠0)是反比例函数，其图象关于原点对称，x=0，y=0为其渐近线方程。

当焦点在x轴上时 双曲线渐近线的方程是y=[+(-)b/a]x。

当焦点在y轴上时 双曲线渐近线的方程是y=[+(-)a/b]x。