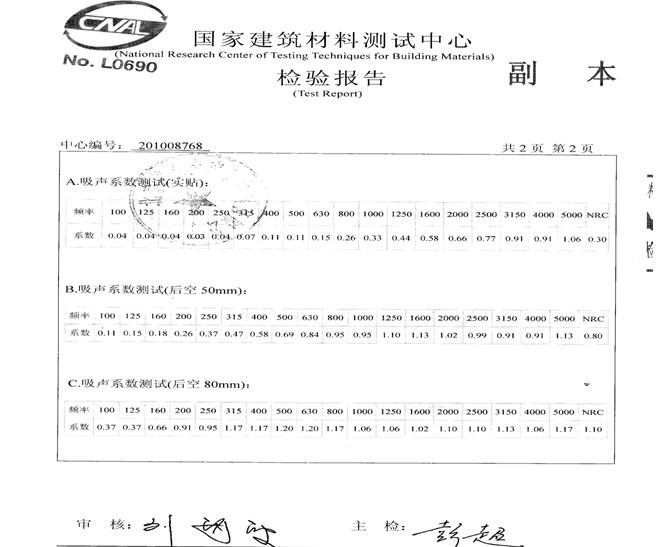
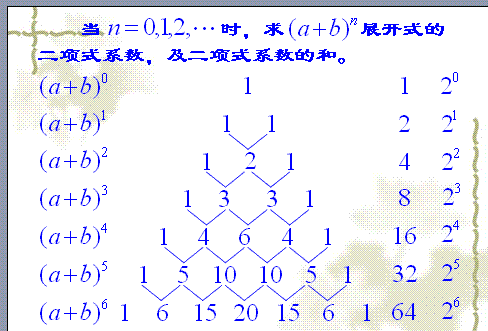
为什么二项式各项系数之和是2^n

为什么二项式各项系数之和是2^n

二项式模型:(1+x)^n

(1+x)^n展开式=c(n,0)1^n+c(n,1)1^(n-1)x+(n,2)1^(n-2)x^2+......+c[n,(n-1)]1^1n^(n-1)+c(n,n)1^0x^n

上面:(1+x)^n展开式中，当x=1时：

c(n,0)1^n+c(n,1)1^(n-1)x+(n,2)1^(n-2)x^2+......+c[n,(n-1)]1^1n^(n-1)+c(n,n)1^0x^n=c(n,0)+c(n,1)+(n,2)+......+c[n,(n-1)]+c(n,n)刚好是二项式(1+x)^n各项的系数和将x=1代入(1+x)^n=c(n,0)1^n+c(n,1)1^(n-1)x+(n,2)1^(n-2)x^2+......+c[n,(n-1)]1^1n^(n-1)+c(n,n)1^0x^n得：

2^n=c(n,0)+c(n,1)+(n,2)+......+c[n,(n-1)]+c(n,n)

故二项式各项系数之和是2^n。

扩展资料：

二项式定理，又称牛顿二项式定理，由艾萨克·牛顿于1664、1665年间提出。此定理指出：首行铅

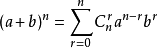 （其中  ）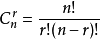

其中，二项式系数指 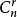等号右边的多项式叫做二项展开式。

二项展开式的通项公式为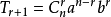 

其i项系数可表示为n取i的组合数目。

赋值法

掌握“赋值法”这种利用恒等式解决问题的思想.

证明：n个a+b相者好乘，是从a+b中取一个字母a或b的积。所以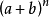 的展开式中每一项都是  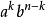)的形式。对于每一个 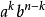，是由k个a+b选了a,a的系数带明为n个中取k个的组合数（就是那个C右上角一个数，右下角一个数）,n-k个a+b选了b得到的（b的系数同理）。由此得到二项式定理。

二项式系数之和：2n

而且展开式中奇数项二项式系数之和等于偶数项二项式系数之和等于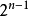 

二项式定理的推广：

二项式定理推广到指数为非自然数的情况：

形式为  .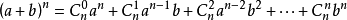

参考资料：二项式_百度百科