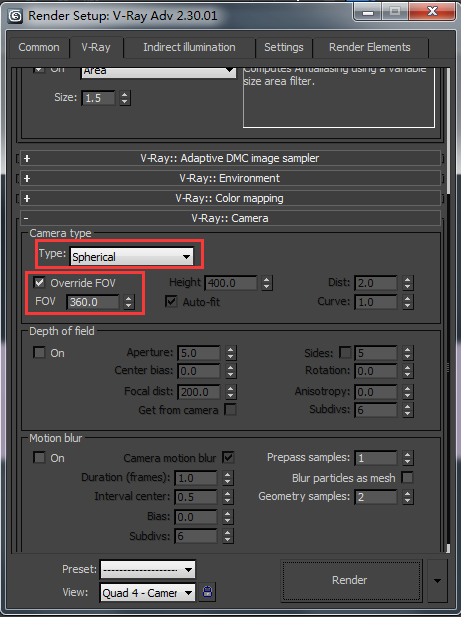
如图，已知抛物线y＝ax平方+bx+3(a不等于0)与x轴交于A(1,0)和点B（-3，0），与y轴

如图，已知抛物线y＝ax平方+bx+3(a不等于0)与x轴交于A(1,0)和点B（-3，0），与y轴

解：(1)由题意知 方程 ax^2+bx+3=0的两根分别是 1，--3 所以 由韦达定理可得：1+（--3）＝--b/a 1*(--3)=3/a 由物链此解得： a=--1,b=--2 所以 所求抛物线的解析式为：y=--x^2-2x+3 （2）抛物线与Y轴交点C的坐标是：C(0,3) 抛物线的对称轴是直线：x=--1,所以M点的坐标是M（--1，0） 因为 点P在对称轴上，所弊蚂御以可设 点P的坐标为（--1，Y.） 则 IPM I=IyI, IPCI=根号里面[1+(y-3）^2 ], IMCI=根号10 因为三角形CMP是等 腰三角形 所以必须是 IPMI=IPCI 或 IPMI=IMCI 或 IPCI=IMCI. 当IPMI=IPCI时 IyI=根号里面[1+(y--3)^2] 即 y^2=1+y^2--6y+9 所以 y=5/3 当IPMI=IMCI时 IyI=根号10 所以 y=根号10 或 y=--根号10. 当IPCI=IMCI时 1+(y--3)^2=10 即 y^2--6y=0 所以 y=0或 y=6 所以说 在对称轴上是存在一点P使三角形CPM为租岩等腰三角形 点P的坐标是(--1,5/3) 或 （--1，根号10）或 （--1，--根号10）或 （--1，6）