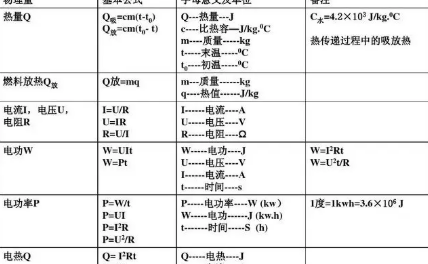
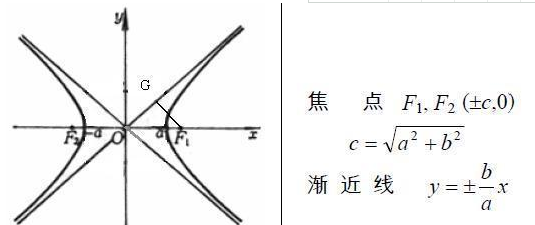
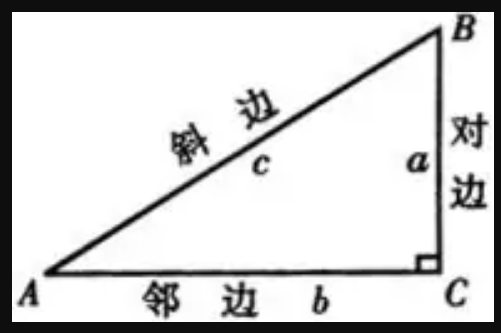
挠度的公式

挠度的公式

细长物体（如梁或柱）的挠度是指在变形时其轴线上各点在该点处轴线法平面内的位移量。薄板或薄壳的挠度是指中面上各点在该点处中面法线上的位移量。物体上各点挠度随位置和时间变化的规律称为挠度函数或位移函数。通过求挠度函数来计算应变和应力是固体力学的芦亩研究方法之一。

挠曲线——如图，平面弯曲时，梁的轴线将变为一条在梁的纵对称面内的平面曲线，该曲线称为梁的挠曲线。

挠度计算公式：Ymax=5ql^4/(384EI)(长l的简支梁在均布荷载q作用下，EI是梁的弯曲刚度）

挠度与荷载大小、构件截面尺寸以及构件的材料物理性能有关。

挠度——弯曲变形时横截面形心沿与轴线垂直方向的线位移称为挠度，用γ表示。

转角——弯曲变形时横截面相对其原来的位置转过的角度称为转角，用θ表示。

挠曲线方程——挠度和转角的值都是随截面位置而变的。在讨论弯曲变形问题时，通常选取坐标轴x向右为正，坐标轴y向下为正。选定坐标轴之后，梁各横截面处的挠度γ将配哗雀是横截面位置坐标培早x的函数，其表达式称为梁的挠曲线方程，即γ= f(x) 。

显然，挠曲线方程在截面x处的值，即等于该截面处的挠度。(建筑工程)

挠曲线在截面位置坐标x处的斜率，或挠度γ对坐标x的一阶导数，等于该截面的转角。

关于挠度和转角正负符号的规定：在上图选定的坐标系中，向上的挠度为正，逆时针转向的转角为正。