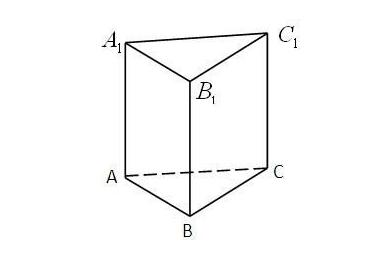
正三棱柱外接球半径怎么求，求详细

正三棱柱外接球半径怎么求，求详细

r=√[(√3/3a)^2+(h/2)^2]。

正三棱柱的外接球:球心为上下底面中心连线中点。

半径为球心与顶点的连线。

设侧棱=h，底面边长为a，底面中心到底面顶点的距离d=√3/3a。

r=√[(√3/3a)^2+(h/2)^2]

扩展资料

正三棱柱的上下底面是全等的两正三角形，侧面是矩形，侧棱平行且相等的棱柱，并且上下底面的中心连线与底面垂直，也就是侧面与底谈宽面垂直。（正三棱柱含于直三棱柱，即正三棱柱是底面是正三角形的直三棱柱）

正三棱柱不一定有内切球：若正三棱柱有内切球,则正三棱柱的高一定是球的直径，此时正三棱柱的棱长为底面边长的(根号3)/3倍；

正含链亮三棱柱一定有外接球：但直径一定不是正三棱柱的高， 直唤耐径为根号(h^2+4a^2/3),其中h为三棱柱的高,a为底面边长。