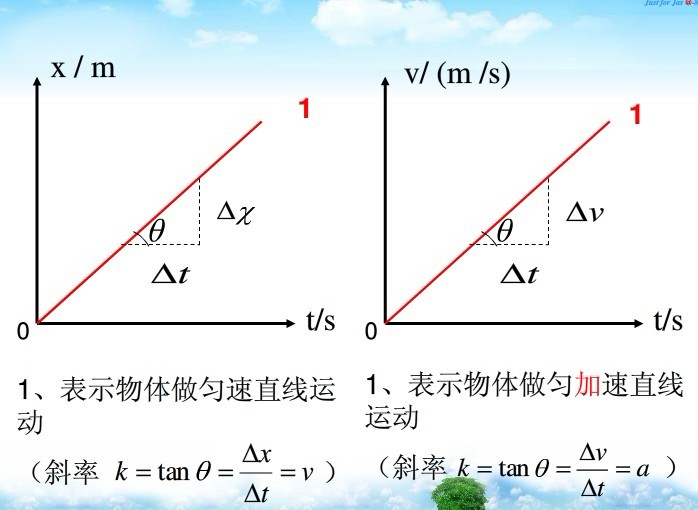
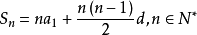已知数列〔an〕

已知数列〔an〕

1(1) a(n+1)=(2an)/(an+1) 1/a(n+1)=(an+1)/2an=(1/2)*(1+1/an) 1/a(n+1)-1=(1/2)*(1/an-1) 所以｛1/an-1}为等比数列! (2) ｛1/an-1}为等比数列! 首项为1/a1-1=1/2 公昌尺大比为1/2 所以：1/an-1=1/2*(1/2)^(n-1)=1/2^n 1/an=1+1/2^n bn=n/an=n*(1/an)=n*(1+1/2^n)=n+n/2^n Sn=1+1/2+2+2/2^2+..+n+n/2^n =1+2+..+n+1/2+2/2^2+...+n/2^n 其中：1+2+...+n=n*(n+1)/2 S=1/2+2/2^2+..+n/2^n S/2=1/2^2+.+(n-1)/2^n+n/2^(n+1) 相减：S/2=1/2+1/2^2+.+1/2^n-n/2^(n+1) =1-1/2^n-n/2^(n+1) S=2-1/2^(n-1)-n/2^n 所以：Sn=1+1/2+2+2/2^2+..+n+n/2^n =1+2+..+n+1/2+2/2^2+...+n/2^n =n*(n+1)/2+2-1/2^(n-1)-n/2^n 21) 因为a3+b5=21,a5+b3=13,{an}是等耐竖差数列,{bn}是等比数列 所以a1+2d+b1*q^4=21,a1+4d+b1*q^2=13 因为a1=b1=1 所以2d+q^4=20,4d+q^2=12 2d+q^4=20方程乘以2得4d+2*q^4=40 用4d+2*q^4=40减去4d+q^2=12得2*q^4-q^2-28=0即(2*q^2+7)*(q^2-4)=0 所困滑以2*q^2=-7或q^2=4 当2*q^2=-7时q^2=-3.5(不符合,舍去) 当q^2=4时q=2或-2 因为bn}是各项都为正数的等比数列 所以q=2 综上所述得q=2 带入4d+q^2得d=2 所以 an=2n-1 bn=2^(n-1) (2) an/bn=(2n-1)/2^(n-1) 叠加 a1/b1=1 a2/b2=3/2 …… sn=1+3/2+5/4+7/8+……(2n-1)/2^(n-1).(1) 2sn=2+3+……+(2n-1)/2^(n-2).（2) (2)-(1),得 sn=6-(4n+6)/(2^n)