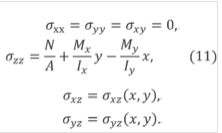求解弹性力学问题的三个基本方程是什么

求解弹性力学问题的三个基本方程是什么

求解弹性力学有类方程，共15个方程。3个平衡方程，6个物理方程，汪前6个几何方程。

弹性力扰罩学是固体力学的重要分支，它研究弹性物体在外力和其他外界因素作用下产生的变形和内力，又称弹性理论。它是材料力学、结构力学、塑性力学和某些交叉学科的基础，广泛应用于建筑、机械、化工、航天等工程领域。

弹性体是变形体的一种，它的特征为：在外力作用下物体变形，当外力不超过某一限度时，除去外力后物体即恢复原状。绝对弹性体是不存在的。物体在外力除去后的残余变形很小时，一般就把它当作弹性体处理。

弹性力学所依据的基本规律有三个：变形连续规律、应力-应变关系和运动(或平衡)规律，它们有时被称为弹性力学三大基本规律。弹性力学中许多定理、公式和结论等，都可以从三大基本规律推导出来。

一、变形连续规律 弹性力学（和刚体的力学理论不同）考虑到物体的变形，但只限于考虑原来连续、变形后仍为连续的物体，在变形过程中，物体不产生新的不连续面。如果物体中本来就有裂纹，则弹性力学只考虑裂纹不扩展的情况。

反映变形连续规律的数学方程有两类：几何方程和位移边界条件。几何方程反映应变和位移的联系，它的力学含义是，应变完全由连续的位移所引起，在笛卡儿坐标系中，几何方程为：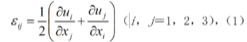

若所考虑的物体Q在其一部分边界B1上和另一物体Q1相连接，而且Q在B1上的位移为已知量，在B1上便有位移边界条件:

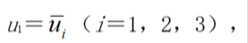
二、应力-应变关系 弹性体中一点的应力状态和应变状态之间存在着一定的联系，这种联系与如何达到这种应力状态和应变状态的过程无关，即应力和应变之间存在一一对应的关系。若应力和应变呈线性关系，这个关系便叫作广义胡克定律，各向同性材料的广义胡克定律有两种常用的数学形式：

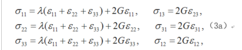和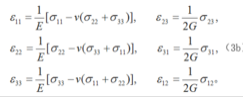

式中为应力分量；λ和G为拉梅常数，G又称剪切模量；E为杨氏模量（或弹性模量）；v为泊松比（见材料的力学性能）。λ、G、E和v四个常数之间存在下列联系：

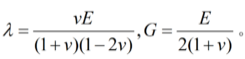
三、运动（或平衡）规律 处于运动（或平衡）状态的物体，其中任一部分都遵守力学中的运动（或平衡）规律，即牛顿运动三定律，反映这个规律的数学方程有两类：运动（或平衡）微分方程和载荷边界条件。在笛卡儿坐标系中，运动（或平衡）微分方程为：

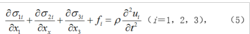
对于均匀而且各缓陵闹向同性的物体，应力分量可按式（3a）用应变分量表示，而应变分量又可按式（1）用位移分量表示。两个公式依次代入方程（5），便得到用位移表示的运动微分方程：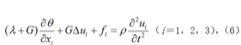

式中θ为体应变，即:

△为拉普拉斯算符，即: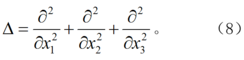

类似地，在方程（6）中略去惯性力，便可得到用位移分量表示的平衡微分方程。

如果考虑物体一部分边界B2是自由的，在它的上面有给定的外载荷，则根据作用力和反作用力大小相等方向相反的原理，在B2上有如下载荷边界条件：

对弹性力学的动力问题，还需说明物体的初始状态，即:

当t=t0时，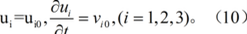

柱体扭转和弯曲 一个侧面不受外力的细长柱体，在两端面上的外力作用下会产生扭转和弯曲。根据圣维南原理，柱体中间部分的应力状态只与作用在端面上载荷的合力和合力矩有关，而与载荷的具体分布无关。因此，柱体中间部分的应力有以下的表达式：